The Venus Bell is so called because its molded shape is a three-dimensionalization of Rudolf Steiner’s Venus seal. The shape of the bell itself is made from the spinning of the seven-sided Chestahedron traced out in time through a full 360 degree rotation.
CUSTOM CREATIONS
Artwork
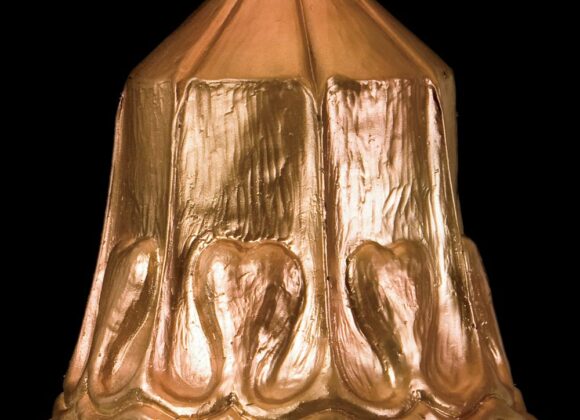
Venus Bell
The Venus Bell is so called because its molded shape is a three-dimensionalization of Rudolf Steiner’s Venus seal. The shape of the bell itself is made from the spinning of the seven-sided Chestahedron traced out in time through a full 360 degree rotation.

Chestahedron
The Chestahedron is the first heptahedron of this configuration in the history of geometry. This sculpture has 7 surfaces (consisting of 4 triangles and 3 quadrilaterals), 7 points and 12 edges.
EXPLORE ART
Gallery
THE HEART
Heartistic Science
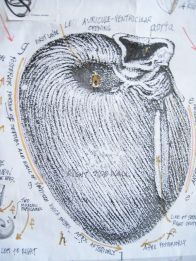
Heartistic Science
By applying an alchemical transformative process to his seven-sided form, Frank has discovered many previously unknown geometric structures that demonstrate a remarkable correlation to the form and functioning of the human heart.

The Heart’s Art
On July 8-11, 2001, keynote speaker Frank Chester presented his remarkable and original research on vortical flow, Platonic solids, and heart geometry.

Threefold Video
Frank Chester’s Michaelmas Talk given on September 29, 2011 at the Threefold Auditorium in Spring Valley, New York. This lecture covers Frank’s insights, based on his research into the new geometry of the heart, into what it means to “defeat the dragon” in our own day and age.
Conferences & Classroom
Video
ABOUT
Frank Chester

Frank Chester
Frank is an artist, sculptor and geometrician based in San Francisco. He has taught art for more than thirty years in high schools and colleges. Since encountering the work of Rudolf Steiner, Frank has been exploring the relation between form and spirit. This site is a space to share his research with the public. Read more...







