The Geometry of the Chestahedron
Make your own chestahedron with this template!
The chestahedron is a unique volume constructed of four equilateral triangles and three “kite” shapes (quadrilaterals). The chestahedron is unique in that the areas of the triangles and quadrilaterals are equal. The chestahedron is the first seven-sided volume with faces of equal area. You can examine one of the ways that the chestahedron is formed out of the transformation of a tetrahedron in this video.
The exact geometry of the chestahedron is known: all the angles in each face and all the dihedral angles (the angles formed when two faces meet). In the video, the chestahedron is formed when the “petals” of the small tetrahedron open up so that their dihedral angle formed with the base triangle is 94.83092. At this point, the area of the quadrilaterals is exactly equal to the area of the equilateral triangles.
The mathematics behind the chestahedron was formulated separately by Dr. Ron Milito as well as Dr. Karl Maret, M.D., and has been subsequently verified independently.
Dr. Ronald Milito has a doctorate in Biophysics, has studied human anatomy in a medical school setting, has done research on cancer detection, and for many years was a teacher of science and mathematics at the college, high school, and middle school levels. Dr. Milito’s solutions will be presented here soon.
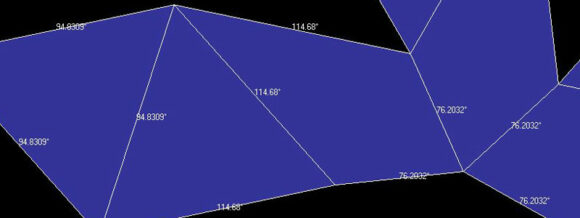
Dr. Karl Maret has used the program Stella 4D to create a digital chestahedron, and has kindly provided images that show the face angles and dihedral angles:
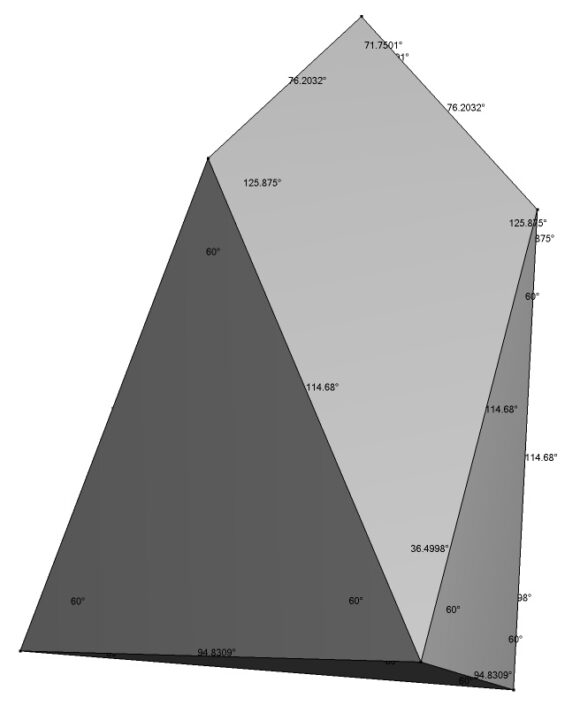
The image above shows the chestahedron with the dihedral angles (the angles formed when faces meet).
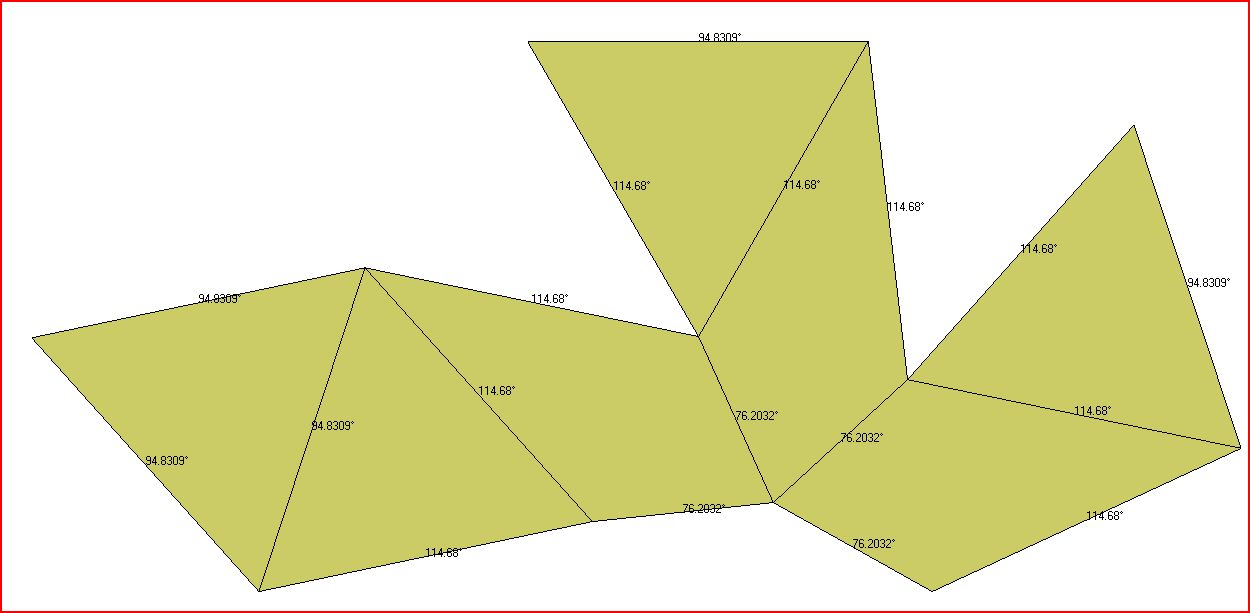
The image above shows the chestahedron as a two-dimensional net, with the dihedral angles (the angles formed when two faces meet).
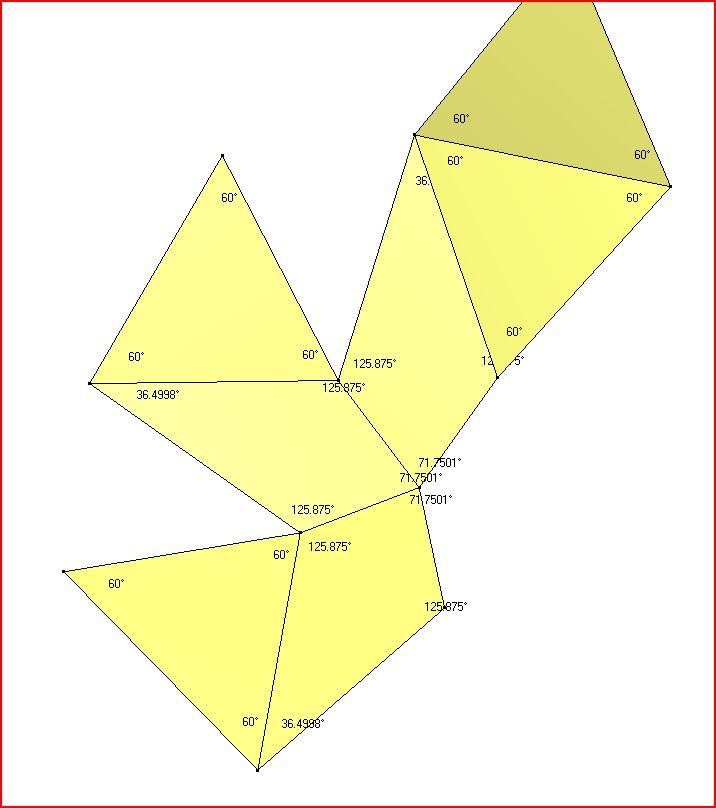
The image above shows the chestahedron as a two-dimensional net with the angles within each face shown.
You must be logged in to post a comment.